Основные определения
ТеорияСистема m линейных алгебраических уравнений с n неизвестными (сокращенно СЛАУ) представляет собой систему вида
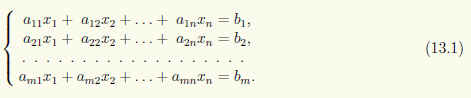
Уравнения системы (13.1) называют алгебраическими потому, что левая часть каждого из них есть многочлен от n переменных x1, ... , xn, а линейными потому, что эти многочлены имеют первую степень.
Числа aij ∈ R называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения i и номером неизвестного j. Действительные числа b1, ..., bm называют свободными членами уравнений.
Запись СЛАУ в виде (13.1) будем называть координатной.
СЛАУ называют однородной, если b1 = b2 = ... = bm = 0. В противном случае ее называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных x°1, ... , х°n, при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют ее частным решением.
Решить СЛАУ — значит решить две задачи:
- выяснить, имеет ли СЛАУ решения;
- найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае ее называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений ее неизвестных всегда является решением. Как показывает следующий пример, для неоднородных СЛАУ возможны различные случаи.
Пример 13.1. Рассмотрим три системы двух уравнений с двумя неизвестными:
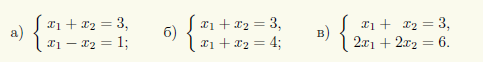
С геометрической точки зрения уравнения каждой из этих СЛАУ задают прямые на плоскости x1Ox2 (рис. 13.1). Решениям СЛАУ соответствуют точки пересечения указанных прямых. Складывая почленно уравнения в первой системе, получаем х1 = 2, х2 = 1 — единственное ее
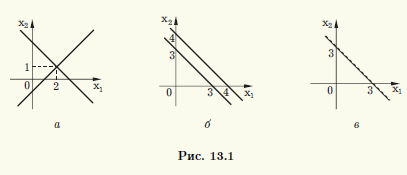
решение. Геометрически это подтверждается тем, что соответствующие прямые пересекаются в единственной точке (2; 1) (рис. 13.1, а). Из уравнений второй системы следует, что 3 = 4. Следовательно, эта СЛАУ несовместна, и геометрически это соответствует двум параллельным несовпадающим прямым (рис. 13.1, б). Наконец, третья СЛАУ такова, что второе ее уравнение является следствием первого: оно получается из первого умножением на 2. Геометрически это означает, что уравнения задают одну и ту же прямую (рис. 13.1, в). Следовательно, координаты любой точки этой прямой удовлетворяют каждому из уравнений системы, т.е. третья СЛАУ совместна и имеет бесконечно много решений. #
Если СЛАУ (13.1) имеет решение, и притом единственное, то ее называют определенной, а если решение неединственное — то неопределенной. При m = n, т.е. когда в (13.1) количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.