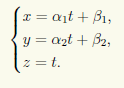Уравнения прямой в пространстве
ТеорияОбщие уравнения прямой в пространстве. Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Если плоскости π1: A1x + B1y + C1z + D1 = 0, π2: A2x + B2y + C2z + D2 = 0 не параллельны, то пересекаются по прямой. Точка M(x; y; z) принадлежит этой прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению каждой из плоскостей, т.е. являются решениями системы уравнений

которую называют общими уравнениями прямой.
Векторное уравнение прямой. Описание прямой в пространстве при помощи общих уравнений — не единственный способ. Прямую L в пространстве можно также однозначно задать любой ее точкой M0 и параллельным ей ненулевым вектором s.
Любой ненулевой вектор, параллельный прямой, называют направляющим вектором прямой.
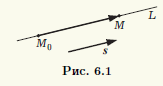
Если точка M принадлежит прямой L, то это эквивалентно тому, что вектор M0M коллинеарен вектору s (рис. 6.1). Так как s ≠ 0, то вектор s является базисом в пространстве V1 коллинеарных ему векторов. Поэтому для некоторого числа t выполняется равенство M0M = ts. Так как M0M = OM — OM0 = r — r0, где r и r0 — радиус-векторы точек M и M0 соответственно, то условие M ∈ L можно записать в виде уравнения
r = r0 + ts, (6.2)
которое называют векторным уравнением прямой в пространстве.
Параметрические уравнения прямой в пространстве. Предположим, что известны координаты {l; m; n} направляющего вектора s прямой L и точки M0(x0; y0; z0) ∈ L в прямоугольной системе координат. Обозначим через (x; y; z) координаты произвольной точки M.
Критерием принадлежности точки M прямой L является условие коллинеарности векторов M0M = {x — x0; y — y0; z — z0} и s (см. рис. 6.1), что равносильно пропорциональности их координат (см. теорему 2.6). Обозначив через t коэффициент пропорциональности, получим равенства x — x0 = tl, y — y0 = tm, z — z0 = tn. Но тогда
 M0M и s, состоящую в пропорциональности их координат (см. следствие 2.1).
M0M и s, состоящую в пропорциональности их координат (см. следствие 2.1).
В знаменателе канонических уравнений допускается нулевое значение. Чтобы понять смысл нулевых значений параметров l, m, n, обратим внимание на параметрические уравнения прямой (6.3), в которых нет проблемы нулевых знаменателей. Например, при l = 0 из (6.3) следует, что x = x0. Мы видим, что если в канонических уравнениях один из знаменателей (или два, но не все три) равен нулю, то соответствующий числитель тоже равен нулю.
Уравнения прямой, проходящей через две точки. Каждая прямая в пространстве однозначно задается любыми двумя своими различными точками. Если известны координаты этих точек M1(x1; y1; z1) и M2(x2; y2; z2), то в качестве направляющего вектора прямой подходит ненулевой вектор M1M2 = {x2 — x1; y2 — y1; z2 — z1}. Зная его координаты и координаты точки M1 на прямой, можно записать канонические уравнения прямой (6.4). В результате получим
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) = (z - z1)/(z2 - z1) -
уравнения прямой, проходящей через две точки.
Пример 6.1. Точки M1(1;2;3) и M2(3; 2; 1) определяют проходящую через них прямую (x - 1)/ (3 - 1) = (y - 2)/ (2 - 2) = (z - 3)/ (1 - 3). Нуль в знаменателе второй дроби означает, что для координат всех точек прямой выполнено равенство y = 2. Поэтому прямая расположена в плоскости y - 2 = 0, параллельной координатной плоскости xOz и пересекающей ось ординат в точке с ординатой 2.
Изменение формы уравнений прямой. Переход от канонических уравнений прямой к параметрическим и обратно достаточно очевиден и сводится к введению или исключению параметра t. Одна форма уравнений непосредственно записывается по другой, так как в них используются одни и те же параметры, задающие координаты точки на прямой и координаты направляющего вектора.
Пример 6.2. Найдем координаты точки B, симметричной точке A(2; 3; — 1) относительно прямой L: (x - 1)/1 = (y + 2)/-1 = (z - 1)/2.
В вычислениях будем опираться на следующее геометрическое построение точки B: а) через точку A проводим плоскость π, перпендикулярную прямой L; б) находим точку M пересечения прямой L и плоскости π; в) отрезок AM удлиняем до отрезка AB так, чтобы точка M оказалась в середине отрезка AB (рис. 6.2).
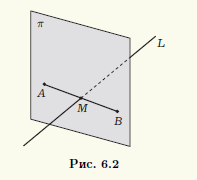
Так как плоскость π перпендикулярна прямой L, то в качестве нормального вектора n плоскости можно выбрать направляющий вектор прямой L: n = {1; — 1; 2}. По известным координатам нормального вектора плоскости п и принадлежащей ей точки A записываем уравнение плоскости π в виде (5.2): 1(х — 2) + (—1)(у — 3) + 2(z + 1) = 0.
Чтобы найти координаты точки M пересечения прямой и плоскости по их уравнениям, запишем параметрические уравнения прямой L: х = 1 + t, у = —2 — t, z = 1 + 2t. Подставив эти выражения для координат точки на прямой в уравнение плоскости, для параметра t получим уравнение (1 + t — 2) — (—2 — t — 3) + 2(1 + 2t + 1) = 0, решение которого дает значение параметра для точки M. Найдя это значение t = —4/3 и подставив его в параметрические уравнения прямой, получим координаты точки пересечения x = 1 — 4/3 = —1/3, у = —2 + 4/3 = —2/3, z =1 — 8/3 = —5/3. Поскольку эта точка должна делить отрезок AB пополам, ее координаты, согласно (4.13), равны полусумме соответствующих координат точек A и B. Следовательно, обозначив через (хB; уB; zB) координаты точки B, получим равенства (2 + xB)/2 = -1/3(3 + yB)/2 = - 2/3(-1 + zB)/2 = -5/3. Отсюда xB = -8/3, yB = -13/3, zB = -7/3#
Достаточно просто выполняется переход от канонических уравнений к общим. Нетрудно увидеть, что на самом деле канонические уравнения представляют собой особую форму записи общих уравнений. Действительно, двойное равенство (6.4) равносильно системе двух линейных уравнений
(x - x0)/l - (y - y0)/m = 0, (x - x0)/l - (z - z0)/n = 0, (6.5)
которые представляют собой частный вид общих уравнений прямой в пространстве.
Самым сложным является переход от общих уравнений к каноническим или параметрическим.
Так как плоскости π1 и π2, соответствующие отдельным уравнениям из общих у (6.1) прямой, не параллельны, то хотя бы один из определителей второго порядка 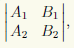
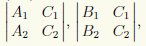 , представляющих собой координаты векторного произведения нормальныхвекторов этих плоскостей, не равен нулю. Предполагая, что первый из этих определителей является ненулевым:
, представляющих собой координаты векторного произведения нормальныхвекторов этих плоскостей, не равен нулю. Предполагая, что первый из этих определителей является ненулевым: 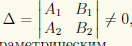 изложим три способа перехода от общих уравнений к каноническим или параметрическим.
изложим три способа перехода от общих уравнений к каноническим или параметрическим.
Первый способ состоит в том, что в системе (6.1) для z назначают два различных значения и по формулам Крамера находят два различных решения системы двух уравнений с двумя неизвестными х и у. Эти два решения системы (6.1) дают координаты двух разных точек M1 и M2 на прямой. А две известные точки прямой позволяют найти уравнение прямой, проходящей через две точки, которое фактически совпадает с каноническими уравнениями прямой.
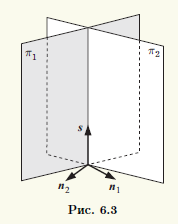
Отметим, что в качестве направляющего вектора s прямой, заданной общими уравнениями (6.1), можно выбрать n1×n2 — векторное произведение двух нормальных векторов плоскостей (рис. 6.3). Действительно, это векторное произведение является вектором, который ортогонален каждому нормальному вектору, а потому он параллелен как одной, так и другой плоскости, т.е. параллелен их линии пересечения. Нахождение одной точки на прямой и ее направляющего вектора можно рассматривать как второй способ перехода от общих уравнений прямой к ее каноническим уравнениям.
Пример 6.3. Найдем канонические уравнения прямой, совпадающей с линией пересечения плоскостей π1: х — у + z — 2 = 0, π2: х + у — z = 0.
Чтобы найти координаты некоторой точки на прямой, подставляем в уравнения плоскостей z = 0 и решаем соответствующую систему двух линейных уравнений относительно х и у
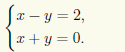
Значения х =1 и у = —1 единственного решения системы получаются сложением и вычитанием уравнений системы. Итак, точка с координатами (1; —1; 0) расположена на прямой.
В качестве направляющего вектора прямой берем векторное произведение n1 × n2 нормальных векторов n1 = {1; — 1; 1} и n2 = {1; 1; —1} плоскостей π1 и π2. По формуле (3.2) для вычисления векторного произведения в координатах находим
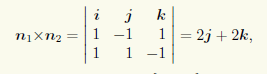
т.е. направляющим вектором прямой будет s = {0;2; 2}. Найденный вектор s для простоты заменим коллинеарным ему вектором {0; 1; 1}.
Проведенные вычисления позволяют написать канонические уравнения искомой прямой
(x - 1)/0 = (y + 1)/1 = z/1. #
Третий способ перехода от общих уравнений прямой к ее каноническим или параметрическим уравнениям состоит в следующем. Решаем систему (6.1) по правилу Крамера относительно неизвестных х и у, рассматривая неизвестное z как параметр:
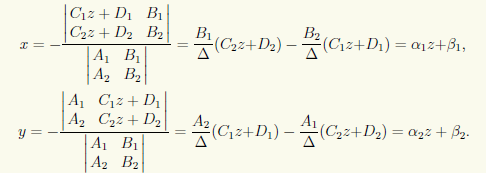
Обозначив z через t и добавив уравнение z = t, получим параметрические уравнения прямой: